Charles Darwin meets Rube Goldberg: a tale of biological convolutedness

Charles Darwin studying a Rube Goldberg Machine (Freepik Generative AI, text-to-image)

For this Darwin Day post (2024), I will discuss the paper Machinery of Biocomplexity [1]. This paper introduces the notion of Rube Goldberg machines as a way to explore biological complexity and non-optimal function. This concept was first highlighted on Synthetic Daises in 2009 [2], while an earlier version of the paper was discussed on Synthetic Daisies in 2013 [3]. The paper was revised in 2014 to include a number of more advanced computational concepts, after a talk to the Network Frontiers Workshop at Northwestern University in 2013 [4]. 

Figure 1. Block and arrow model of a biological RGM (bRGM) that captures the non-optimal changes resulting from greater complexity. Mutation/Co-option removes the connection between A and B, then establishes a new set of connection with D. Inversion (bottom) flips the direction of connections between C-B and C-A, while also removing the output. This results in the addition of E and D which reestablishes the output in a circuitous manner.

Biological Rube Goldberg Machines (bRGNs) are defined as a computational abstraction of convoluted, non-optimal mechanisms. Non-optimal biological systems are represented using flexible Markovian box and arrow models that can be mutated and expanded given functional imperatives [5]. Non-optimality is captured through the principle of "maximum intermediate steps": biological systems such as neural pathways, metabolic reactions, and serial interactions do not evolve to the shortest route but is constrained (and perhaps even converge to) the largest number of steps. This results in a set of biological traits that functionally emerge as a biological process. Figure 1B shows an example where maximal steps represents a balance between the path of least resistance and exploration given constraints on possible interconnections [6]. The paths from A-E, E-B, and C-D are the paths of least resistance given the constraints of structure and function. In the sense that optimality is a practical outcome of physiological function, a great degree of intermediacy can preserve unconventional pathways that are utilized only spontaneously.

This can be seen in a wide variety of biological systems and is a consequence of evolution. Evolutionary exaptation, the evolution of alternative functions, and serial innovation all result in systems with a large number of steps from input to output. But sometimes convolution is the evolutionary imperative in and of itself. As fitness criteria change over evolutionary time, traces of these historical trajectories can be observed in redundant pathways and other results of subsequent evolutionary neutrality. One example from the paper involves a multiscale model (genotype-to-phenotype) that exploits both tree depth and lateral connectivity to maximize innovation in the production of a phenotype (Figure 2). While our models are based on connections between discrete states, bRGMs can also provide insight into the evolution of looser collections of single traits and even networks, where the sequence of function is bidirectional and hard to follow in stepwise fashion.

Figure 2.  A hypothetical biological RGM representing a multi-scale relationship. Each set of elements (A-F) represents the number of elements at each scale (actual and potential connections are shown with bold and thin lines, respectively). Examples of convolutedness incorporate both loops (as with E5,1 and E5,5) and the depth of the entire network.

The paper also features extensions of the basic bRGM, including massively convoluted architectures and microfluidic implementations. In the former, interconnected networks represent systems that are not only maximal in terms of size or length, but also massively topologically complex [7]. One example of this is cortical folding and the resulting neuronal connectivity in Mammalian brains. The latter example is based on fluid dynamics and combinatorial architectures that are more in line with discrete bRGMs (Figure 3). 

Figure 3. A microfluidic-inspired bRGM model that mimics the complexity of biological fluid dynamics (e.g. blood vessel networks). G1, G2, and G3 represent iterations of the system.

References:

[1] Alicea, B. (2014). The "Machinery" of Biocomplexity: understanding non-optimal architectures in biological systems. arXiv, 1104.3559.

[2] Non-razors, unite! January 30, 2009. https://syntheticdaisies.blogspot.com/2009/01/non-razors-unite.html

[3] Maps, Models, and Concepts: July Edition. Synthetic Daises blog. July 13, 2013. https://syntheticdaisies.blogspot.com/2013/07/maps-models-and-concepts-july-edition.html

[4] Inspired by a visit to the Network's Frontier....  Synthetic Daises blog. December 16, 2013. https://syntheticdaisies.blogspot.com/2013/12/fireside-science-inspired-by-visit-to.html

[5] when dealing with a large number of steps or in a polygenic context, these types of models can also resemble renormalization groups. For more on renormalization group, please see: Wilson, K.G. (1975). Renormalization group methods. Advances in Mathematics, 16(2), 170-186.

[6] this balance is as predicted by Constructive Neutral Evolution (CNE). For a relevant paper, please see: Gray et.al (2010). Irremediable Complexity? Science, 330(6006), 920-921.

[7] in the paper, this is referred to as Spaghettification, a term borrowed from the physics of gravitation. See this reference for an interesting implementation of this in soft materials:  Bonamassa et.al (2024). Bundling by volume exclusion in non-equilibrium spaghetti. arXiv, 2401.02579.

Ancient Embryogenesis and Evolutionary Origins

"Darwin as an Embryo". In this case, Neoteny really does recapitulates Phylogeny! COURTESY: Stable Diffusion.

For this year's delayed Darwin Day post, I will present some of the latest work on ancient embryos which we have been discussing in the DevoWorm group meetings. While this is by no means a complete review, we will discuss the earliest fossil evidence for eggs, embryos, and nervous systems (in animals, not plants), in addition to the conditions that lead to their emergence. In short, how did we get to embryos from a universal common ancestor with bacteria and archebacteria, and why do only different types of Eukaryotes (plants, radial symmetrical Metazoans, and bilateral Metazoans) have embryos?

Tree of Life (genome tree) from Hug et.al [1] with three domains. Click to enlarge.

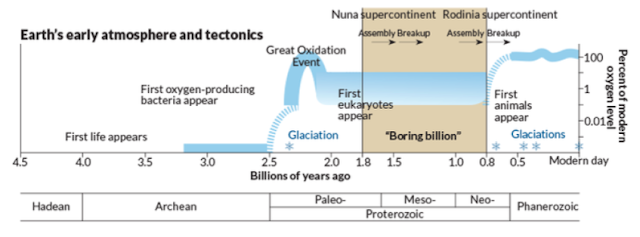
The ecological states of early Earth. COURTESY: J. Hirshfeld/Wikimedia. Click to enlarge.

We begin in the Cambrian, where the firs bilaterian appeared around 600 million years ago, approximately 70-80 million years before the Cambrian explosion [2]. In between the emergence of bilaterians, several key innovations occurred that suggests the origins of embryos and egg-laying. The first are the presence of fossilized burrows [2] for egg-laying behaviors. By the end of the Cambrian explosion, early pancrustecean arthropod species were possibly subject to life-history tradeoffs related to clutch size [3]. Another key innovation is direct evidence in the form of well-preserved multicellular structures from the period leading up to the Cambrian explosion that show a transition in cell geometry from a 2-cell stage to a cleavage stage [4]. As representative of a variety of ancestral algae species from the Doushantuo formation, these remains have not been connected to any particular adult form. However, they do demonstrate oogenesis and cleavage [2]. Finally, the functional genomics of developmental pattern formation emerged during this time [5]. This includes a ProtoHox cluster in ancestral cnidarians [6], Hox gene duplication [7], and an increase in body size and shape diversity alongside the advent of bilaterian bauplans [8]. Multiple Hox gene families may have served the role of promoting directed locomotion that in turn promoted active exploration of the environment [7].

Images of a potential early embryo, including the 2-cell and cleavage stages [from 4]. Click to enlarge.

The Ediacaran (630-540 million years ago) has yielded a large number of potential embryonic forms. In the Ediacaran biota, we find a number of Metazoan remains with no clear phylogenetic position. However, Evans et.al [9] propose that early embryos evolved independently (with several origins) in the bilaterian clade. However, during this time, a number of general trends emerge that enabled modern bilaterian adult forms. As previously discussed, Multicellular structures with distinct cell types, axial polarity, and anatomical segmentation [10, 11] emerged during this time. Left-right symmetry was a related feature of these embryos [11]. So-called polarized elements [12] such as microtubules, flagella, and apical-to-basal orientation were all found soon after the last Eukaryotic common ancestor (LECA). The evolution and diversification of polarity proteins is consistent with this timeline [12]. Other organismal structures such as a gut, sub-specialization of the phenotype, and a nervous system with heads and appendages are also features of note. We will talk about the emergence of nervous systems later on.

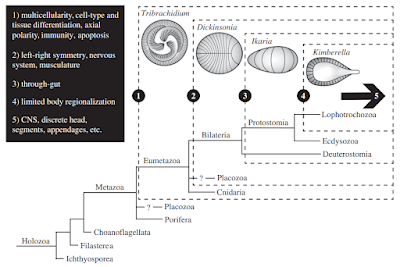
Scenario for the origins of development in bilaterians from [9]. Click to enlarge.

Bicellum brasieri is a 10⁹ year old fossil holozoan that might provide the very earliest examples of modern embryos and embryogenesis [13]. Microfossils of Bicellum demonstrate morphogenesis in the form of cell-cell adhesion for different cell types, as well as differential layers of cells (driven by adhesion) which may be the precursors of tissue differentiation. This can be compared to the Doushantuo embryos from Precambrian China [14], and Caveasphera from 609 million years ago [15], which are perhaps the direct ancestors of Metazoan embryonic forms. These are the first examples of development proceeding within an enclosed space, enabled by cell adhesion similar to what is observed during gastrulation in modern embryos. Caveasphera in particular shows evidence of anatomical polarization (particularly polar aggregation), cell division events, and ingression [15]. This is informative but is not diagnostic of the Urmetazoan condition [16].

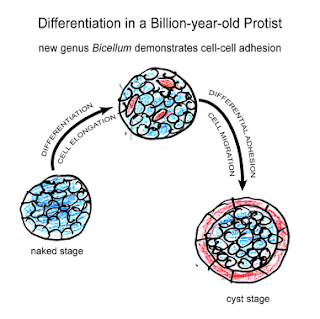
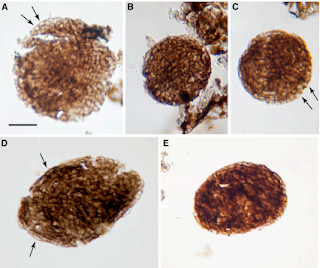
Graphical abstract and (top) palynological evidence of Bicellum brasieri (bottom) as shown in [13]. Epidermal layer (A and C), ellipsoid (D) and oblate (E) specimens Click to enlarge.

Since these pre-Cambrian explosion phenotypes are very simple, we can look to fossil evidence for much more complex embryo phenotypes in the late Cretaceous. Xing et.al [17] report on an in-ovo therapod dinosaur embryo, where the body is folded into an elongated egg. The authors are able to demonstrate how the fully formed head and legs are folded into different prehatching postures.

Graphical abstract showing developmental stages of Caveasphera [15]. Click to enlarge.

While the early phylogeny of nervous system origins is the very definition of a tangled tree [18], the first nervous systems coincide with the emergence of discrete body types in the Cambrian [19]. Brains emerged in part from the developmental toolkit responsible for patterning and segmentation [20]. This toolkit consists of genes and regulatory mechanisms that were co-opted for the development of excitable cells [21], synapses [22], and neuronal networks [2]. While the strongest evidence for early embryos only show evidence for bilaterian organization, radial symmetry is actually the basal condition for Metazoans [23]. Therefore, early embryos should yield at least two types of nervous system configurations that are observed in modern phenotypes: a centralized nervous system that converges in the head (the brains of bilaterians), and a distributed nervous system (the nerve nets of cnidarians). Centralized nervous systems originated from the mesoderm layer of triploblastic embryos, while distributed nervous systems are derived from the endoderm of diploblastic embryos. While there is a distinct literature on fossil radial embryos from China [24], there does not seem to be fossil evidence of germ layers formation and subsequent differentiation in any early embryos to date.

Image of Baby Yingliang (therapod dinosaur late-stage embryo) [17]. Click to enlarge.

But what happened before the earliest embryos (1000-650 million years ago)? What ecological conditions might have driven this innovation? One trigger may have been the great oxygenation event, which occurred in two stages: the first at 2.4 billion years ago, and the second at 950 million years ago. It was the second event that increased oxygen content to a level more resembling the present, and in turn drove diversification of distinct fungi, plants, and animals. It is of note that LECA (the last Eukaryotic common ancestor) lies well-beforehand [25]. The earliest embryos (or at least multicellular packings) might have resulted from selection pressure for retaining a low-oxygenation environment. But while these findings may lead to significant speculation, it seems that embryos are unique to Eukaryotic evolution, having no Bacterial or Archaebacterial counterpart despite evolving under the same conditions. It is most likely the interaction of genomic factors, developmental contingencies, and environmental conditions that ultimately lead to the emergence of embryos [26].

Phylogeny with evolution transitions from LUCA to embryos in plants and animals. Included are the two oxygenation events of Earth's history. Transitions derived from Refs [14, 27-31]. Click to enlarge.

References

[1] Hug, L.A. et.al (2016). A new view of the tree of life. Nature Microbiology, 1, 16048. 

[2] Valentine, J.W., Jablonski, D., and Erwin, D.H. (1999). Fossils, molecules and embryos: new perspectives on the Cambrian explosion. Development, 126, 851-859.

[3] Ou, Q., Vannier, J., Yang, X., Chen, A., Mai, H., Shu, D., Han, J., Fu, D., Wang, R., and Mayer, G. (2020). Evolutionary trade-off in reproduction of Cambrian arthropods. Science Advances, 6(18), doi:10.1126/sciadv.aaz3376.

[4] Xiao, S., Zhang, Y. and Knoll, A. H. (1998). Three-dimensional preservation of algae and animal embryos in a Neoproterozoic phosphorite. Nature, 391, 553-558.

[5] Erwin, D.H. (2020). Origin of animal bodyplans: a view from the regulatory genome. Development, 147, dev182899. 

[6] Chourrout, D. et al. (2006). Minimal ProtoHox cluster inferred from bilaterian and cnidarian Hox

complements. Nature, 442, 684–687. 

[7] Holland, P.W.H. (2015). Did homeobox gene duplications contribute to the Cambrian explosion? Zoological Letters, 1, 1. 

[8] Zhuravlev, A.Y. and Wood, R. (2020). Dynamic and synchronous changes in metazoan body size during the Cambrian Explosion. Scientific Reports, 10, 6784. 

[9] Evans, S.D., Droser, M.L., Erwin, D.H. (2021). Developmental processes in Ediacara macrofossils. Royal Society B, 288, 20203055.

[11] Finnerty, J.R., Pang, K., Burton, P., Paulson, D., and Martindale, M.Q. (2004). Origins of bilateral

symmetry: Hox and Dpp expression in a sea anemone. Science, 304, 1335–1337.

[12] Brunet, T. and Booth, D.S. (2023). Cell polarity in the protist-to-animal transition. Current Topics in Developmental Biology, doi:10.1016/bs.ctdb.2023.03.001.

[13] Strother, P.K., Brasier, M.D., Wacey, D., Timpe, L., Saunders, M., and Wellman, C.H. (2021). A possible billion-year-old holozoan with differentiated multicellularity. Current Biology, 31, 1–8.

[14] First Embryos: Chen, J-Y., Bottjer, D.J., Li, G., Hadfield, M.G., Gao, F., Cameron, A.R., Zhang, C-Y., Xian, D-C., Tafforeau, P., Liao, X., and Yin, Z-J. (2009). Complex embryos displaying bilaterian characters from Precambrian Doushantuo phosphate deposits, Weng’an, Guizhou, China. PNAS, 106(45), 19056-19060.

[15] Yin, Z., Vargas, K., Cunningham, K., Bengtson, S., Zhu, M., Marone, F., and Donoghue, P. (2019). The Early Ediacaran Caveasphaera Foreshadows the Evolutionary Origin of Animal-like Embryology. Current Biology, 29, 4307–4314.

[16] Sebe-Pedros, A., Degnan, B.M., and Ruiz-Trillo, I. (2017). The origin of Metazoa: a unicellular perspective. Nature Reviews Genetics, 18, 498–512.

[17] Xing, L., Niu, K., Ma, W., Zelenitsky, D.K., Yang, T-R., and Brusatte, S.L. (2021). An exquisitely preserved in-ovo theropod dinosaur embryo sheds light on avian-like prehatching postures. iScience, 103516.

[18] Miller, G. (2009). On the Origin of The Nervous System. Science, 325(5936), 24-26.

[19] Erwin, D.H. (2020). Origin of animal bodyplans: a view from the regulatory genome. Development, 147, dev182899. 

[20] Hartenstein, V. and Stollewerk, A. (2015). The evolution of early neurogenesis. Developmental Cell, 32, 390–407.

[21] Moroz, L.L. and Kohn, A.B. (2016). Independent origins of neurons and synapses: insights from ctenophores. Royal Society B, 371, 20150041.

[22] Moroz, L.L. (2021). Multiple Origins of Neurons From Secretory Cells. Frontiers in Cell and Developmental Biology, 9, 669087. 

[23] Ghysen, A. (2003). The origin and evolution of the nervous system. International Journal of Developmental Biology, 47(7-8), 555-562.

[24] Xian, X-F., Zhang, H-Q., Liu, Y-H., and Zhang, Y-N. (2019). Diverse radial symmetry among the Cambrian Fortunian fossil embryos from northern Sichuan and southern Shaanxi provinces, South China. Palaeoworld, 28(3), 225-233.  AND  Chang, S., Clausen, S., Zhang, L., Feng, Q., Steiner, M., Bottjer, D.J., Zhang, Y., Shi, M. (2018). New probable cnidarian fossils from the lower Cambrian of the Three Gorges area, South China, and their ecological implications. Palaeogeography, Palaeoclimatology, Palaeoecology, 505, 150-166.

[25] McGrath, C. (2022). Highlight: Unraveling the Origins of LUCA and LECA on the Tree of Life. Genome Biology and Evolution, 14(6), evac072.

[26] Erwin, D.H. (2021). Developmental capacity and the early evolution of animals. Journal of the Geological Society, 178(5), jgs2020-245.

[27] Archaea: Gribaldo, S. and Brochier-Armanet, C. (2006). The Origin and Evolution of Archaea: a state of the art. Royal Society B, 361, 1007-1022.

[28] Great Oxygenation Event: Knoll, A.H.and Nowak, M.A. (2017). The Timetable of Evolution. Science Advances, 3, e1603076.  AND   Erwin, D.H. (2015). Early metazoan life: divergence, environment and ecology. Royal Society B, 370, 20150036.

[29] Fungi-Animal Common Ancestor: Phelps, C., Gburcik, V., Suslova, E., Dudek, P., Forafonov, F., Bot, N., MacLean, M., Fagan, R.J., and Picard, D. (2006). Fungi and animals may share a common ancestor to nuclear receptors. PNAS, 103(18), 7077–7081.

[30] LUCA: Dodd, MS, Papineau, D, Grenne, T et al. (5 more authors) (2017). Evidence for early life in Earth’s oldest hydrothermal vent precipitates. Nature, 543 (7643). pp. 60-64.  AND  Hassenkam, T., Andersson, M., Dalby, K., MacKensie, D.M.A., and Rosing, M.T. (2017). Elements of Eoarchean life trapped in mineral inclusions. Nature, 548, 78–81.

[31] Tree of Life: Feng, D-F., Cho, G., and Doolittle, R.F. (1997). Determining divergence times with a protein clock: Update and reevaluation. PNAS, 94, 13028-13033.

Gyrification of the Tree of Mammals

For this year's Darwin Day post, I will be reviewing the evolutionary origins and developmental emergence of gyrification of the Mammalian brain. Gyrification occurs when the neocortex, or six layered cortex on the dorsal surface of Mammalian brains, exhibits wrinkles and folds rather than a smooth surface (lissencephaly). Gyrification is measured using the gyrification index (or GI). GI can range from 5.6 in Pilot whales (Globicephala) to 3.8 in Elephants (Loxodonta) and 2.6 in Humans (Homo) [1]. A more extensive phylogenetic analysis (Figure 1) shows the evolutionary trajectory for this in Hominids, and a highly gyrified brain is associated with other traits that emerge as early as the divergence of Primates. 

Figure 1. A phylogeny of primate brain evolution (with Mammalian outgroups), with a focus on the origin of traits found in the human brain. COURTESY [2].

The evolutionary origins of gyrification may either be mono- or polyphyletic, as different genes have been identified as potential associated factors. Gyrification might also be a product of convergent evolution, as this trait may simply be a by-product of larger neocortical sheets. Steidter [3] points out that gyrification may simply be due to physical constraints related to fitting a vastly enlarged cortical sheet into a skull scaled to an organism's body size. 

Figure 2. Allometric scaling across select Mammalian brain, showing an increase in gyrification for larger brains. COURTESY [4].

In Figure 2, we see that in general larger brains also have a larger GI value. The curvilinear relationship shown in the figure is known as an allometric scaling. Allometry [5] is a convenient way to quantitatively assess relative growth across different species, and the resulting regression parameters are suggestive of underlying mechanisms that control and predict growth across evolution.

In this case, the allometric relationship is brain size versus tangential expansion. Tangential matter is expansion of gray matter relative to the constraints of white matter, or a grey-to-white matter proportion [4]. As the amount of gray matter increases, brain size also tends to increase, and so does the GI value. However, the proportion of gray to white matter saturates, while brain sizes continue to expand along with increasing GI values. 

Figure 3. Simulating gyrification as a by-product of physical processes. 3-D printed models based on MRI data for brains from different stages of development. COURTESY [6].

Genetic analyses implicate the role of specific genes in controlling brain volume, which then sets the stage for gyrification [7]. Developmental mutations in the human genetic loci collectively known as MCPH 1-18 [8] lead to a condition called microcephaly, where the mature microcephalic brain remains small and lacks gyrification. In a study of 34 species [9], the largest source of explained variance between species can be explained by random Brownian motion. Furthermore, the data within the order Primates shows that fold wavelength is stable (~12mm) despite a 20-fold difference in volume [9]. 

As an alternative hypothesis to evolutionary origins, gyrification can result from various physical processes in developmental morphogenesis (Figure 3). The gyrification process consists of gyral (ridge-like) and sulcal (groove-like) convolutions. In the earliest stages of development, no gyrification is expressed in the phenotype. However, as the neocortex grows faster relative to the rest of the brain, a mechanical instability results that leads to buckling [6]. Buckling thus creates gyrification, although the consistency of their localization and timing in development suggests underlying cellular and molecular mechanisms. Demonstration of biophysical mechanisms does not preclude a phylogenetic explanation, however. As we will see later on, surface physics relies upon the presence of certain cell types and growth conditions.

Figure 4. An overview of the evolution of development (Evo-Devo) of gyrification. Gyrification and lissencephaly occur through mechanisms that affect changes in brain size and GI relative to the last common ancestor (in this figure, transitional form). COURTESY [10].

There are also several cellular and molecular factors that contribute to neocortical growth, and thus towards gyrification. In Figure 4, we see four archetypes that result from increases and decreases of brain size coupled with increases and decreases of GI. For example, increases in basal radial ganglion (bRG) precursor cells and transit-amplifying progenitor cells (TAPs) contribute to increases of both brain size and GI [10]. Decreases in brain size and GI are controlled by changes in cell cycle timing and associated heterochronic changes. Heterochrony has to do with the timing of the rate and termination of growth in development and is but one factor that suggests lissencephaly is actually the derived condition. Thus, smooth brains would be an evolutionary reversal from the ancestral gyrified state that occurred multiple times across the tree of Mammals. 

Once again, an evolutionary conundrum. Happy evolutioning!

NOTES:

[1] Johnson, S. Number and Complexity of Cortical Gyrii. Center for Academic Research and Training in Anthropogeny. La Jolla, CA. Accessed: February 13, 2022. 

[2] Franchini, L.F. (2021). Genetic Mechanisms Underlying Cortical Evolution in Mammals. Frontiers in Cell and Developmental Biology, 9, 591017.

[3] Striedter, G. (2005). Principles of brain evolution. Sinauer, Sunderland, MA.

[4] Tallinen, T., Chung, J.Y. , Biggins, J.S., and Mahadevan, L. (2014). Gyrification from constrained cortical expansion. PNAS, 111(35), 12667-12672.

[5] Shingleton, A. (2010) Allometry: The Study of Biological Scaling. Nature Education Knowledge, 3(10), 2.

[6] Tallinen, T., Chung, J.Y., Rousseau, F., Girard, N., Lefevre, J., and Mahadevan, L. (2016). On the growth and form of cortical convolutions. Nature Physics, 12, 588–593.

[7] Zilles, K., Palomero-Gallagher, N., and Amunts, K. (2013). Development of cortical folding during evolution and ontogeny. Trends in Neurosciences, 36(5), 275-284. 

[8] Jayaraman, D., Bae, B-I., and Walsh, C.A. (2018). The Genetics of Primary Microcephaly. Annual Review of Genomics and Human Genetics, 19, 177-200.

[9] Heuer, K., Gulban, O.F., Bazin, P-L., Osoianu, A., Valabregue, R., Santin, M., Herbin, M., and Toro, R. (2019). Evolution of neocortical folding: A phylogenetic comparative analysis of MRI from 34 primate species. Cortex, 118, 275-291.

[10] Kelava, I., Lewitus, E., and Huttner, W.B. (2013). The secondary loss of gyrencephaly as an example of evolutionary phenotypical reversal. Frontiers in Neuroanatomy, 7, 16.

Assorted Darwin Day Content

For this year's Darwin Day post, I will highlight a number of items I have recently run across on Twitter. Some of these have been retweeted on the Orthogonal Research and Education Lab Twitter feed, other materials are related to discussions in our research group meetings.

To start things off, I will draw your attention to a new special issue of Royal Society of London B called "Basal cognition: multicellularity, neurons and the cognitive lens" that is worth checking out. The term "basal" refers to evolutionary origins in the context of phylogeny (the tree of life). 

There are three papers of particular note for Darwin Day: "The chemical brain hypothesis for the origin of nervous systems" by Gaspar Jekely, "Elementary Nervous Systems" by Detlev Arendt, and "Uncovering cognitive similarities and differences, conservation and innovation" by Michael Levin and colleagues.

The new paper on elementary nervous systems in Royal Society B (click to enlarge, figure from paper). COURTESY: Detlev Arendt.

A pointer to the Darwin Online repository.

In terms of old drawings and other archival materials, check out the Darwin Online project. This is a nice repository of Darwin-related historical and scientific works. This resource contains books, personal correspondence, and published materials. Speaking of history, let's turn to the deep history of life.....

A billion years of continental drift as an animated gif. Click to enlarge.

This next feature is a new paper on a billion years of plate tectonic dynamics: "Extending full-plate tectonic models into deep time: Linking the Neoproterozoic and the Phanerozoic" by Mike Tetley and colleagues. Now published in Earth Science Reviews, it is something we recently discussed in the weekly DevoWorm group meeting.

Following up on the DevoWorm discussion, which was about mapping the continental drift animation to the most basal branches of the tree of life, is an attempt to map Mammalian phylogeny [1] to continental drift over the past 225 million years. This was created by Carlos E. Alvarez. The numbers on the maps (top) correspond to the numbered clades (subtrees - bottom). This topic deserves a deeper dive into the latest Phylogeography research [2], which may be the subject of a future blog spot.

An attempt at matching up the tree of life with continental drift (click to enlarge). COURTESY: Carlos E. Alvarez

The next feature is a new paper on evolution of development (evo-devo) in nervous system anatomy called "Evolution of new cell types at the lateral neural border", now published in Current Topics in Developmental Biology. This study even uses converging evidence from genetic regulatory networks and anatomy to demonstrate common mechanisms shared between invertebrates and vertebrates.

A new paper on the evolution of new neuronal cell types (click to enlarge). COURTESY: Jan Stundl (Caltech).

Not only is this Darwin Day, but also the 50th anniversary of a Nature paper by Kimura and Ohta [3] on the Neutral Theory of Molecular Evolution. Neutral Theory postulates that most biological variation is expressed in selectively neutral genes, and so is random in nature [4]. This stands in opposition to the selectionist perspective of evolutionary change [5, 6].

Fully-tweetable neutral theory of evolution. COURTESY: Andrew J. Crawford.

Finally, and returning to neuroevolution, there are several items of interest from the laboratory of Cassandra Extavour. The first is a talk at the Society of Integrative and Comparative Biology meeting on the evo-devo-eco-neuro-biology of Drosophila learning and memory. For more evo-devo work from Dr. Extavour's lab, check out this recent work (with open data) on insect size and shape [7, 8].

Original artwork from SICB Twitter Account, commentary from Ken A. Field.

Hand-drawn notes on the SICB plenary talk. COURTESY: Dr. Ajna Rivera.

NOTES:

[1] Foley N.M., Springer M.S. and Teeling E.C. (2016). Mammal madness: is the mammal tree of life not yet resolved? Philosophical Transactions of the Royal Society B, 37120150140. doi:10.1098/ rstb.2015.0140.

[2] Avise, J.C. (2000). Phylogeography: the history and formation of species. Harvard University Press, Cambridge, MA.

[3] Kimura, M. and Ohta, T. (1971). Protein Polymorphism as a Phase of Molecular Evolution. Nature, 229, 467–469.

[4] Kimura, M. (1983). The Neutral Theory of Molecular Evolution. Cambridge University Press, Cambridge, UK.

[5] Nei, M. (2005). Selectionism and Neutralism in Molecular Evolution. Molecular Biology and Evolution, 22(12), 2318–2342. doi:10.1093/molbev/msi242.

[6] There are other critiques of selectionism from other perspectives. Here is one in the area of brain function: Fernando, C., Szathmary, E., and Husbands, P. (2012). Selectionist and Evolutionary Approaches to Brain Function: A Critical Appraisal. Frontiers in Computational Neuroscience, 6, 24. doi:10.3389/ fncom.2012.00024.

[7] Church, S.H., Donoughe, S., de Medeiros, B.A.S., and Extavour, C.G. (2019). Insect egg size and shape evolve with ecology but not developmental rate. Nature, 571, 58–62.

[8] Church, S.H., Donoughe, S., de Medeiros, B.A.S., and Extavour, C.G. (2019). A dataset of egg size and shape from more than 6,700 insect species. Scientific Data, 6, 104.

Sperry, Darwin, and the Evolution of Reference Frames

It's all about deforming the phenotype. COURTESY: DiPaola, Evolving Darwin's Gaze (click to enlarge).

For this year's Darwin Day (February 12), I will be discussing a classic Neuroscience experiment by Roger Sperry [1]. This was discussed recently on Twitter (Figures 1 and 3), along with a movie (Movie 1) that demonstrates the behavioral effect of this manipulation. In the movie, we can see before and after behaviors with respect to prey capture. Before the manipulation, the frog seamlessly captures flies with a flick of the tongue. Afterward, the frog flicks in precisely the opposite direction of the fly. What is the biology behind this manipulation, and why does the manipulation produce seemingly maladaptive behavior?  

Figure 1. Tweet on Sperry's eye rotation experiment and chemosensory hypothesis (click to enlarge). 

Movie 1. Video demonstration of Sperry's eye rotation experiment (click to enlarge). 

In conducting this experiment, a frog's eyes are surgically rotated 180 degrees about each socket (see Figure 2). Due to this treatment, the normal course of axonogenesis between the eyeball and the tectum (part of the frog brain) is distorted [2]. As a result, the connections are shifted and the visual information is mapped to different regions of the tectum. The tectum serves as a visuospatial map of the environment, and maps visual stimuli to a reference frame used to generate motor behavior. As the reference frame is than systematically rotates, so is the frog's movement behavior. Thus, our manipulated frog produces a tongue flick that is 180 degrees in the opposite direction of the prey it is trying to capture. 

Figure 2. Cartoon demonstrating chemosensory hypothesis and behavioral effects of eye rotation experiment (click to enlarge). 

What is known as the chemosensory hypothesis (see Figure 2) also provided support for another concept, that of experience-dependent plasticity. The second tweet (below) discusses how this concept explains (and does not explain) what we see in the frog tectum and its modified behavior.

Figure 3. Part of response to tweet in Figure 1, with an assessment of the functional consequences (click to enlarge). 

Roger Sperry is also known for another set of experiments conducted a few years later [3] that asked whether neuroplasticity was a real phenomenon (as opposed to an epiphenomenon). This was done by either abnormally innervating muscle or placing end-effectors (limbs) in maladaptive locations on the body. If the organism could overcome these changes, such changes could be overcome via adaptation. As in the case of the eye rotation experiment, motor patterns are not plastic, even when neuronal connections are non-specific. This is why the eye rotated frog cannot adjust its behavior to adaptation in the spatial representation of visual input. 

Figure 4. A demonstration of conduction delay in the quadruped hindlimb in relation to multiple components of the sensorimotor loop. COURTESY: Figure 1 in [7] (click to enlarge).

So what does this have to do with evolution by natural selection [4]? It turns out that there are scaling laws that govern the coordination of the nervous system and phenotype as they both emerge in development [5]. Specifically, there are characteristically proportional relationships between motor neuron innervation and target tissue size in different parts of the organism [5, Note 1]. This developmental relationship (which holds true across related species) leads to interesting functional consequences. More et.al [6] suggests a trade-off in sensorimotor systems between responsiveness (temporal respond to stimuli) and resolution (sensory discrimination translated into muscle force production) results from size variation across phylogeny. 

Figure 5. Scaling of various sources of delay across species. Scaling comparison is in terms of mass (kg) versus delay (ms). COURTESY: Figure 2 in [7] (click to enlarge).

This relationship between size and a responsiveness-resolution trade-off also affects behavior. More and Donelan [7] show that conduction delay (an indicator of reaction time) also scales with variation in organismal size (Figure 4). The delay in force production (behavioral output) can be explained mostly in terms of nerve conduction delay rather than a delay in the sensory or synaptic components of the sensorimotor loop (Figure 5). This suggests a fundamental constraint on motor behavior that is independent of sensory inputs or their neural representation. But notice what is said about frog tectum in Figure 3: while eye saccades and tongue movement that produce the movement itself are not controlled by the tectum, a triggering threshold results from the active representation of visual information. 

Through the efficiency of population coding [8], this representation determines the timing of movement execution, which occurs in spatial context along with an appropriate amount of force. Perhaps the rotated eye manipulation (and associated phenomena like the prism experiment) presents an interesting exception to the responsiveness/resolution trade-off. Perhaps an intervening variable, representational alignment, also affects the linearity of the primary trade-off for specific movement behaviors. Across different species with common ancestry [9], this could become quite variable, and even provide an evolutionary-based account of neural plasticity.

NOTES:

[1] Sperry, R.W. (1943). Effect of 180 Degree Rotation of the Retinal Field on Visuomotor Coordination. Journal of Experimental Zoology, 92(3), 263–279.

[2] the reference to chemoaffinity in the first tweet refers to the process of axons finding their way to a target tissue. This is the basis for Sperry's "chemoaffinity hypothesis". Please see: Meyer, R.L. (1998). Roger Sperry and his chemoaffinity hypothesis. Neuropsychologia, 36 (10), 957–980.

[3] Sperry, R.W. (1945). The Problem of Central Nervous Reorganization After Nerve Regeneration and Muscle Transposition. Quarterly Review of Biology, 20(4), 311-369.

[4] For more on this topic, please see the following Synthetic Daisies posts:

     The Evolution and Neuromechanics of very-fast movements. January 24, 2012

     The Neuromechanics and Evolution of Very Slow Movements. April 18, 2012

     Perceptual Time and the Evolution of Informational Investment. September 24, 2013

[5] Striedter, G.F. (2004). Principles of Brain Evolution. Oxford University Press, Oxford, UK.

[6] More, H.L., Hutchinson, J.R., Collins, D.F., Weber, D.J., Aung, S.K.H., and Donelan, J.M. (2010). Scaling of sensorimotor control in terrestrial mammals. Royal Society of London B, 277(1700), 3563-3568.

[7] More, H.L. and Donelan, J.M. (2018). Scaling of sensorimotor delays in terrestrial mammals. Royal Society of London B, 285(1855), 20180613.

[8] Shamir, M. (2014). Emerging principles of population coding: in search for the neural code. Current Opinion in Neurobiology, 25, 140-148 AND Pouget, A., Dayan, P., & Zemel, R. (2000). Information processing with population codes. Nature Reviews Neuroscience, 1, 125–132.

[9] Quian Quiroga, R. (2019). Neural representations across species. Science, 363(6434), 1388-1389.

Darwin meets Category Theory in the Tangential Space

For this Darwin Day (February 12), I would like to highlight the relationship between evolution by natural selection and something called category theory. While this post will be rather tangential to Darwin's work itself, it should be good food for thought with respect to evolutionary research. As we will see, category theory also has relevance to many types of functional and temporal systems (including those shaped by natural selection) [1], which is key to understanding how natural selection shapes individual phenotypes and populations more generally.

This isn't the last you'll hear from me in this post!

Category Theory originated in the applied mathematics community, particularly the "General Theory of Natural Equivalence" [2]. In many ways, category theory is familiar to those with conceptual knowledge of set theory. Uniquely, category theory deals with the classification of objects and their transformations between mappings. However, category theory is far more powerful than set theory, and serves as a bridge to formal logic, systems theory, and classification.

A category is defined by two basic components: objects and morphisms. An example of objects are a collection of interrelated variables or discrete states. Morphisms are things that link objects together, either structurally or functionally. This provides us with a network of paths between objects that can be analyzed using categorical logic. This allows us to define a composition (or path) by tracing through the set of objects and morphisms (so-called diagram chasing) to find a solution.

In this example, a pie recipe is represented as a category with objects (action steps) and morphisms (ingredients and results). This monoidal preorder can be added to as the recipe changes. From [3]. Click to enlarge.

Categories can also consist of classes: classes of objects might include all objects in the category, while classes of morphism include all relational information such as pathways and mappings. Groupoids are functional descriptions, and allow us to represent generalizations of group actions and equivalence relations. These modeling-friendly descriptions of a discrete dynamic system is quite similar to object-oriented programming (OOP) [4]. One biologically-oriented application of category theory can be found in the work of Robert Rosen, particularly topics such as relational biology and anticipatory systems.

Animal taxonomy according to category theory. This example focuses on exploring existing classifications, from species to kingdom. The formation of a tree from a single set of objects and morphisms is called a preorder. From [3]. Click to enlarge.

One potential application of this theory to evolution by natural selection is to establish an alternate view of phylogenetic relationships. By combining category theory with feature selection techniques, it may be possible to detect natural classes that correspond to common ancestry. Related to the discovery of evolutionary-salient features is the problem of phylogenetic scale [5], or hard-to-interpret changes occurring over multiple evolutionary timescales. Category theory might allow us to clarify these trends, particularly as they relate to evolving life embedded in ecosystems [6] or shaped by autopoiesis [7]. 

More relevant to physiological systems that are shaped by evolution are gene regulatory networks (GRNs). While GRNs can be characterized without the use of category theory, they also present an opportunity to produce an evolutionarily-relevant heteromorphic mapping [8]. While a single GRN structure can have multiple types of outputs, multiple GRN structures can also give rise to the same or similar output [8, 9]. As with previous examples, category theory might help us characterize these otherwise super-complex phenomena (and "wicked" problems) into well-composed systems-level representations.

NOTES:
[1] Spivak, D.I. (2014). Category theory for the sciences. MIT Press, Cambridge, MA.

[2] Eilenberg, S. and MacLane, S. (1945). General theory of natural equivalences. Transactions of the American Mathematical Society, 58, 231-294. doi:10.1090/S0002-9947-1945-0013131-6 

[3] Fong, B. and Spivak, D.I. (2018). Seven Sketches in Compositionality: an invitation to applied category theory. arXiv, 1803:05316.

[4] Stepanov, A. and McJones, P. (2009). Elements of Programming. Addison-Wesley Professional.

[5] Graham, C.H., Storch, D., and Machac, A. (2018). Phylogenetic scale in ecology and 
evolution. Global Ecology and Biogeography, doi:10.1111/geb.12686.

[6] Kalmykov, V.L. (2012). Generalized Theory of Life. Nature Precedings, 10101/npre.2012.7108.1.

[7] Letelier, J.C., Marin, G., and Mpodozis, J. (2003). Autopoietic and (M,R) systems. Journal of Theoretical Biology, 222(2), 261-272. doi:10.1016/S0022-5193(03)00034-1.

[8] Payne, J.L. and Wagner, A. (2013). Constraint and contingency in multifunctional gene regulatory circuits. PLoS Computational Biology, 9(6), e1003071. doi:10.1371/journal.pcbi.1003071.

[9] Ahnert, S.E. and Fink, T.M.A. (2016). Form and function in gene regulatory networks: the structure of network motifs determines fundamental properties of their dynamical state space. Journal of the Royal Society Interface, 13(120), 20160179. doi:10.1098/rsif.2016.0179.

Darwin as a Universal Principle

Background Diagram: Mountian-Sky-Astronomy-Big-Bang blog.

For this year's Darwin Day post, I would like to introduce the concept of Universal Darwinism. To understand what is meant by universal Darwinism, we need to explore the meaning of the term as well as the many instances Darwinian ideas have been applied to. The most straightforward definition of Universal Darwinism is a Darwinian processes that can be extended to any adaptive system, regardless of their suitability. Darwinian processes can be boiled down to three essential features:

1) production of random diversity/variation (or stochastic process).  

2) replication and heredity (reproduction, historical contingency). 

3) natural selection (selective mechanism based on some criterion). 

A fourth feature, one that underlies all three of these points, is the production and maintenance of populations (e.g. population dynamics). These features are a starting point for many applications of universal Darwinism. Depending on the context of the application,these four features may be emphasized in different ways or additional features may be added.

Taken collectively, these three features constitute many different types of process, encompassing evolutionary epistemology [1] to cultural systems [2], neural systems [3, 4], physical systems [5, 6], and informational/cybernetic systems [7, 8]. Many of these universal applications are explicitly selectionist, and do not have uniform fitness criteria. In fact, fitness is assumed in the adaptive mechanism. This provides a very loose analogy to organismal evolution indeed.

Universal computational model shaped by Darwinian processes. COURTESY: Dana Edwards, Universal Darwinism and Cyberspace.

Of these, the application to cybernetic systems is the most general. Taking inspiration from both cybernetics theory and the selectionist aspects of Darwinian models, Universal Selection Theory [7, 8] has four basic claims that can be paraphrased in the following three statements:

1) "operate on blindly-generated variation with selective retention". 

2) "process itself reveals information about the environment". 

3) "processes built atop selection also operate on variation with selective retention".

The key notions are that evolution acts to randomly generate variation, retains only the most fit solutions, then builds upon this in a modular and hierarchical manner. In this way, universal Darwinian processes act to build complexity. As with the initial list of features, the formation and maintenance of populations is an important bootstrapping and feedback mechanism. Populations and heredity underlie all Darwinian processes, even if they are not defined in the same manner as biological populations. Therefore, all applications of Darwinian principles must at least provide an analogue to dynamic populations, even at a superficial level.

There is an additional advantage of using universal Darwinian models: capturing the essence of Darwinian processes in a statistical model. Commonalities between Darwinian processes and Bayesian inference [3, 5] can be proposed as a mechanism for change in models of cosmic evolution. In the Darwinian-Bayesian comparison, heredity and selection are approximated using the relationship between statistical priors and empirical observation. The theoretical and conceptual connections between phylogeny, populations, and Bayesian priors is a post-worthy topic in and of itself.

At this point, we can step out a bit and discuss the origins of universal Darwinian systems. The origin of a Darwinian (or evolutionary) system can take a number of forms [9]. There are two forms of "being from nothingness" in [9] that could be proposed as origin points for Darwinian systems. The first is an origin in the lowest possible energetic (or in our case also fitness) state, and the other is what exists when you remove the governance of natural laws. While the former is easily modeled using variations of the NK model (which can be generalized across different types of systems), the latter is more interesting and is potentially even more universal.

An iconic diagram of Cosmic Evolution. COURTESY: Inflation Theory by Dr. Alan Guth.

An iconic diagram of Biological Evolution. COURTESY: Palaeontological Scientific Trust (PAST).

So did Darwin essentially construct a "theory of everything" over 200 years ago? Did he find "42" in the Galapagos while observing finches and tortoises? There are a number of features from complexity theory that might also fit into the schema of Darwinian models. These include concepts from self-organization not explicitly part of the Darwinian formulation: scaling and complexity, dependence on initial condition, tradeoffs between exploitation and exploration, and  order arising from local interactions in a disordered system. More explicitly, contributions from chaos theory might provide a bridge between nonlinear adaptive mechanisms and natural selection.

The final relationship I would like to touch on here is a comparison between Darwinian processes and Universality in complex systems. The simplest definition of Universality states that the properties of a system are independent of the dynamical details and behavior of the system. Universal properties such as scale-free behavior [10] and conformation to a power law [11] occur in a wide range of systems, from biological to physical and from behavioral to social systems. Much like applications of Universal Darwinism, Universality allows us to observe commonalities among entities as diverse as human cultures, organismal orders/genera, and galaxies/universes. The link to Universality also provides a basis for the abstraction of a system's Darwinian properties. This is the key to developing more representationally-complete computational models.

8-bit Darwin. COURTESY: Diego Sanches.

Darwin viewed his theory development of evolution by natural selection as an exercise in inductive empiricism [12]. Ironically, people are now using his purely observational exercise as inspiration for theoretical mechanisms for systems from the natural world and beyond.


NOTES:
[1] Radnitzky, G.,‎ Bartley, W.W., and Popper, K. (1993). Evolutionary Epistemology, Rationality, and the Sociology of Knowledge. Open Court Publishing, Chicago. AND Dennett, D. (1995). Darwin's Dangerous Idea. Simon and Schuster, New York.

[2] Claidiere, N., Scott-Phillips, T.C., and Sperber, D. (2014). How Darwinian is cultural evolution? Philosophical Transactions of the Royal Society B, 36(9), 20130368.

[3] Friston, K. (2007). Free Energy and the Brain. Synthese, 159, 417-458.

[4] Edelman, G.M. (1987). Neural Darwinism: the theory of neuronal group selection. Oxford University Press, Oxford, UK.

[5] Campbell, J. (2011). Universal Darwinism: the path to knowledge. CreateSpace Independent Publishing.

[6] Smolin, L. (1992). Did the universe evolve? Classical and Quantum Gravity, 9, 173-191.

[7] Campbell, D.T. (1974). Unjustified Variation and Selective Retention in Scientific Discovery. In "Studies in the Philosophy of Biology", F.J. Ayala and T. Dobzhansky eds., pgs. 139-161. Palgrave, London.

[8] Cziko, G.A. (2001). Universal Selection Theory and the complementarity of different types of blind variation and selective retention. In "Selection Theory and Social Construction", C. Hayes and D. Hull eds. Chapter 2. SUNY Press, Albany, NY.

[9] Siegal, E. (2018). The Four Scientific Meanings Of ‘Nothing’. Starts with a Bang! blog, February 7.

[10] Barabási, A-L. (2009). Scale-Free Networks: a decade and beyond. Science, 325, 412-413.

[11] Lorimer, T., Gomez, F., and Stoop, R. (2015). Two universal physical principles shape the power-law statistics of real-world networks. Scientific Reports, 5, 12353.

[12] Ayala, F.J. (2009). Darwin and the Scientific Method. PNAS, 106(1), 10033–10039.