Fluid Models of Evolutionary Dynamics

Supplementary information for papers from "Fluid Models of Evolutionary Dynamics" project: 

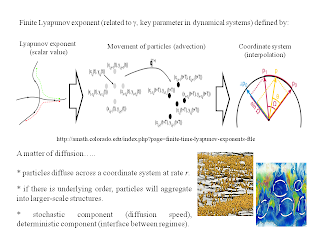
Major features of the Lagrangian Coherent Structures (LCS) approach

Lagrangian Coherent Structures arise from the dynamics of a second-order Lagrangian system. The nature, structure, and emergence of these are demonstrated in the following slides:

A Lagrangian is a special type of dynamical system that accounts for motion constraints imposed on a system of particles with respect to their potential energy. This is a particularly useful context within which to simulate and evolve evolutionary systems, as motion allows us to characterize analogues to evolutionary distance, evolutionary populations, and divergence rate for problems such as evolvability and cultural evolution. While these problems require a search space, they also require a simple space that the well-known fitness landscape approach does not provide.

Identifying Lagrangian Coherent Structures in purely physical systems involves “tracking” aggregations of particles in flow fields. In my LCS-inspired analogy for biological and cultural evolution presented here, we can calculate similar summary statistics: the finite-time Lagrangian exponent (FTLE), which measures divergence with respect to time, and the finite-space Lagrangian exponent (FSLE), which measures divergence with respect to space. 

In both cases, the exponent is a scalar value which can tell us about the divergence of any two particles in the flow field. For applications to evolutionary systems, this can be useful for tracking individuals within and between populations, or for averaging within and between entire populations.

In nature, there are many instances of these structures. While the structures (e.g. streaks, tracks, vortex rings, and streams) are themselves qualitative, individual particles or even features can be quantitatively characterized.

Contextual Geometric Structures (application to evolutionary dynamics in cultural systems):
Contextual Geometric Stuctures (CGS - application to cultural complexity). Paper (Proceedings of Artificial Life, 13) and Presentation.

Figure 1. Process model (Frames A-E) demonstrating the process of evolution in a CGS (or LCS-like biological model).

Figure 2. Features of the soft classificatory kernel, with examples from a number of real-world examples (e.g. taste, pain, feelings).

Figure 3. Mapping the soft classificatory kernels (left) to the flow field, where Lagrangian Coherent Structures are formed (right). 

CGS models are a hybrid model that combines soft classificatory structures* with a LCS-inspired, n-dimensional evolutionary landscape (Figures 1-3). This model is used to evolve cultural structures that characterize distinct cultural traditions. An animation of cultural evolution using two different types of classificatory structure is shown in Animation 1. Animation 1 demonstrates a typical particle simulation over the course of 35 iterations. The initial population is 9 automata (five 5-tuples - 0.55 of population, and four 3-tuples - 0.45 of population).

Animation 1: typical LCS-inspired 2-dimensional volume populated with automata (two different types of soft classification kernels - white shapes).

* the structure of these soft automata (see paper for examples) are based on interval-valued fuzzy logic [1].

There are four features of note:

* CGS models are abstract representations of individuals, which are shown as polygons. These polygons are automata that carry a representation of certain cultural structures.

* the 2-dimensional flow field component of the CGS model is a metric space. Therefore, diffusion across this space can be measured and divergence between all particles can be directly compared.

* the automata in CGS models are also subject to replication (not shown in animation).

* each automata starts off in an initial cluster (shown in Figures 4 and 5) and diffuses within the space according to the defined flow (Figure 6).

Figure 4. The divergence of two automata from a single initial population (cluster). In this case (laminar flow), the divergence is characterized as the arc between the two arrowheads. In a more turbulent flow, the paths of divergence would be less straight.

Figure 5. The convergence of two automata from different initial populations (clusters). The divengence is characterized as the arc between the two arrowheads. In this case, two automata starting out in different points have converged to a nearly identical position (negative divergence). This example also shows dynamic behavior under laminar flow conditions.

Figure 6. Flow jets (bars along boundary) and flows (arrows) for a 2-dimensional flow field.

The LCS-inspired flow field is generated using a set of flow rules. A flow field is required for diffusion of particles, and is a generalized stand-in for environment. In fluid dynamics, turbulent flows (or flows with large Reynolds number) produce the most interesting dynamics. In the model presented here, flow conditions can be created by using rulesets that specify the location, number, and strength of flows into the field. 

Flow jets (shown in Figure 6) are located along the field boundary, and the subsequent flows mediate the diffusion of particles. These flow conditions supervise the evolution of particles in the simulation, but depending on the turbulence produced do not lead to deterministic behavior.

Figure 7. Graph (using pseudo-data) showing the relationship between the degree of turbulence created using the flow jets and the step size per iteration for automata embedded in the flow field.

Figure 7 theoretically demonstrates the expected relationship between:

* the degree of turbulence produced using a particular set of rules governing the location and strength of the flow jets.

* the number of step sizes taken by automata embedded in the flow field. 

As we can see from the graph, configurations that result in laminar flows (left side of graph) result in a consistent step size across the simulation. Meanwhile, configurations that result in highly turbulent flows (right side of graph) result in a highly variable step size both for the trajectory of single automata and the paths between automata. Since this is a physically-inspired model, this can be characterized by a degree of turbulence, which is proportional but not exactly equivalent to changes in Reynolds number [2].

References:

[1] Nguyen, H.T. and Walker, E.A. (1999). A First Course in Fuzzy Logic. CRC Press, New York.

[2] Golestanian, R., Yeomans, J.M., and Uchida, N. (2011). Hydrodynamic synchronization at low Reynolds number. Soft Matter, 7, 3074-3082.

Bounded Evolvability (application to evolvability in biological systems):

Lagrangian Coherent Strucutres (LCS) may describe evolvable frontiers in natural populations (application to biological evolution). Paper (arXiv).

Figure 8. Basic overview of the LCS-like biological model. Panels A, B, and C show a defined trait space, while B and C demonstrate the beginning and end of a particle automata evolution scenario. Insets show the particle genomes (left) and evolutionary process (right).

Figure 9. Conceptual demonstration and description of evolvable boundaries concept.

The LCS-like biological model can also be used to model different aspects of biological evolution as well. In this case, particle automata are homogeneous with regard to internal structure (e.g. no soft kernels), but contain a simple genome that governs replication and survival in various flow conditions (Figure 8). Particles are seeded in an n-dimensional environment (representing the phenotypic variance defined by a series of traits), and allowed to evolve under diffusion conditions. Strict diffusion is analogous to random genetic drift (e.g. neutral evolution) [1]. This allows us to model a series of evolutionary scenarios, ranging from biogeographical evolution to population-level neutral processes.

The main feature of the featured application, however, is to detect the limits of evolvability [2] in a defined population (Figure 9). In this case, coherent structures represent statistical frontiers of the population. Statistical frontiers, which are inspired by frontier analysis in economics [3], represent optimization along different dimensions of the space. In short, evolvable frontiers represent the maximal degree of evolutionary exploration over a given period of time. While this is useful for examining a number of scenarios involving biological populations, it may also be a useful approach in conjunction with the CGS model for studying phenomena such as creativity or the generation of novel behaviors.

References:

[1] Hu, T. and Banzhaf, W. (2009). Neutrality and Variability: two sides of evolvability in linear genetic programming. Proceedings of GECCO, 963-970.

[2] Wagner, A. (2005b). Robustness, evolvability, and neutrality. FEBS Letters, 579, 1772-1778.

[3] Farrell, M.J. (1957). The Measurement of Productive Efficiency. Journal of the Royal Statistical
Society A, 120, 253–281.

Practical Examples of how the CGS model can approximate cultural evolution:

1) Cultural contact. The meeting of two cultures, such as European colonization of the new world or an influx of immigrants into a host country, may be characterized using this technique. In this case, differences between cultures are gradient-like, with uneven discontinuities between the two ancestral cultures (e.g. the amount of intermingling is expected to be heterogeneous). Geographic and qualitative differences are distilled to geometric sorting under common conditions. This sorting allows us to observe whether different cultural traditions intermingle to form common aggregations or segregate to form independent aggregations.

2) Intentional distinction. The segregation and mutual exclusion of two cultures may be characterized using this technique. In this case, the boundary between cultures is intentionally sharp, being the product of sorting with respect to an imposed boundary. Examples of this include national boundaries and residential segregation. Geographic and qualitative differences are distilled to geometric sorting under variable conditions.

3) Fundamentalism. The extreme intentional distinction between two cultures, with one being the self-proclaimed “pure” group may be characterized using this technique. Examples of this include religious cults and extremist political movements. The attributes of the intentional distinction example also hold for the fundamentalist example. However, in terms of the CGS model, a feedback is required between the soft classifications that characterize the automata structural memory and the population-level flow field aggregation.

From the CGS Model (classification component) to Cultural Exemplars:

In human societies, what is the unit of analysis for understanding the structures of a specific culture? In many cases, this unit of analysis is the smallest component of culture that still has basic relations of the entire culture.

An example from the Kayapo of South America focuses on kinship [1]. The unit of analysis for kinship is the domestic unit, which consists of familial relations within a single household. These relations can be reproduced at larger scales, such as the village or regional settlement patterns. 

More generally, what are structures, and how do they relate to the n-dimensional soft kernels in the CGS model? To provide concrete examples of cultural structures, we can turn to the thoughts and observations of cultural anthropologists. 

David Graeber [2]: 
Structures can be defined as a hidden code that ties everything in a culture together. Each structure is defined by how value is allocated to specific concepts or natural phenomena. For example, a structure can consist of concepts such as “wealth”, “sacredness”, or ”thrift”.

In some societies (such as the Kabyle of North Africa), kinship (relatedness) and economy (exchange) are part of the same structure. In other societies, politics (allocation of power) and religion (divination) are part of the same structure.

Pierre Bourdieu [3]: 
Among the Kabyle, the structure of economy consists of wealth along two dimensions: economic (cattle ownership) and social (prestige). In general, structures allocate people, relationships, and natural phenomena as oppositional pairs (e.g. either 'A' or 'B'), and constitutes the normal order of life. 

Bourdieu also proposed something called the “habitus” to describe the enveloping nature of these structures. Behaving within these structures, or engaging in a practice, is beyond the conscious awareness of the individual.

As conceptualized, the CGS model cuts across these definitions to relate such cultural structures to neural computational structures related to cognition. In the CGS model, a structure (or n-dimensional kernel) is generally at a lower level of abstraction than what is proposed in the examples from culture. However, the CGS model includes contextual anchors that link lower-level sensory and linguistic oppositions [4] with higher-level cultural oppositions. In particular, the soft classification scheme allows for an approximation of higher-level complexity. A potential feedback mechanism between the classificatory and evolutionary components of the CGS model is to evaluate how much these classifications change over time across a population of individuals.

References:

[1] Mayberry-Lewis, D. (1979). Dialectical Societies: Ge and Bororo of Central Brazil.  

[2] Graeber, D. (2001). Toward An Anthropological Theory of Value.

[3] Bourdieu, P. (1990). The Logic of Practice.

[4] Lakoff, G.and Johnson, M. (1980). Metaphors We Live By.

Practical Examples of how the LCS-like biological model can approximate evolvable systems:

1) General Biogeography. As with the CGS model, LCS-like biological models inherently contain a quasi-geography. This can be extended from geometric distances and relationships to the introduction of spatial barriers which influence flow dynamics and restrict diffusion. In LCS-like biological models, these barriers can be used to model complex biogeographical scenarios.

2) Reseeding (for genetic drift and island biogeography). For a number of neutral evolutionary scenarios, the environment must be reseeded. This is certainly the case with demographic bottlenecks, in which the restriction of gene flow due to reproductive isolation must be accounted for. In the figure below, a single coherent structure is treated as a subsample. The space is reinitialized using only these particle automata in the same location. Diffusion proceeds from this point, and influences future evolvability.

Outstanding Issues:

Relationship between cognition and structures:

A bit outside the context of the CGS model is the relationship between cultural structures and cognitive function. However, this discussion will help to clarify the relationship between structures used in this simulation and active cognitive control. Figure 10 shows the potential fluctuation between cultural structures and cognition. In short, we live in structures, but live with cognition, which leads to the following hypothesis:

H: the observed dysfunction of some cultural systems is actually a mismatch between structures and cognition.

When practitioners operate on structures, they do so in the absence of information sufficient for cognitive control. However, these structures often do not match the current context. Conversely, practitioners might switch from structures to cognition (e.g. situational behavior) if structures are sparse.

Figure 10: The relationship between structures and cognition

Additional issues:

There are two additional issues that limit the full implementation of the CGS model, both involving feedback mechanisms. 

* the first of these involves the relationship between the soft classification spaces that constitute the automata’s structural memory and the formation of structures in the flow field. 

* the second involves feedback between the soft classification spaces and the flow rules. The current architecture only allows for open-ended flows to affect the diffusion of automata, which then leads to aggregations in the flow field. 

In the real world, however, cultural structures can be changed intentionally by agents exhibiting cognition. This model limits the agency of individuals and replaces it with a stochastic component. While this is likely sufficient in many cases, it can be problematic for modeling some scenarios involving rapid cultural change.