Synthetic Daisies: Saturday Morning NeuroSim Discussion Thread: Physical Computing

From the “Macy Conference Redux” feature form our July 1 meeting

Over the past three years, the Saturday Morning NeuroSim group has met weekly on Saturdays (mornings in North America). The Saturday Morning format continues in the tradition of Saturday Morning Physics and covers a wide variety of topics.

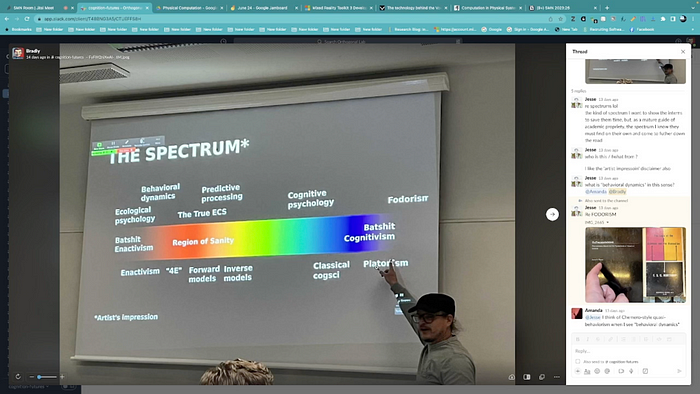
One recent lecture/discussion thread is on Physical Computation. Our approach to the topic begins with the debate around the role of computation in Cognitive Science and the Neurosciences. And so we begin in Week 1 with a discussion of the connections between computation, information processing, and the brain, largely focusing on the work of Gualtiero Piccinini and Corey Maley. A starting point for this session is their Stanford Encyclopedia of Philosophy article on “Computation in Physical Systems”. Many current assumptions about computation in the brain stem from the Church-Turing thesis, which often leads to a poor fit between model and experiment. Piccinini and Maley propose that the Church-Turing-Deutsch thesis is preferable when talking about systems that perform non-digital computations. Amanda Nelson pointed out the it makes sese to think of evolved biological systems (brains) as instances of analogue computers. Another interesting point from the session is the distinction between the digital (Von Neumann) computers and alternatives such as “physical” or “analog” computation, which would be picked up on in the next session.

Physical Computation Session I from June 24 (roughly one hour in length).

The second session focused on physical computation, and led us to discuss the idea of pancomputationalism. While pancomputationalism is the fundamental assumption behind the phrase “the brain is a computer” [1], we we also introduced to pancomputationalism in ferrofluidic systems and mycelial networks. We discussed the works of Richard Feynman (Feynman Lectures on Computation) and Edward Fredkin (Digital Physics), which helped us form an epistemic framework for computation in nature [2]. We also discussed Andy Adamatsky’s work on unconventional computation, particularly his work on Reaction-Diffusion (R-D) Automata, that while discrete in nature has connections to excitable (e.g neural) systems via the Fitzhugh-Nagumo model.

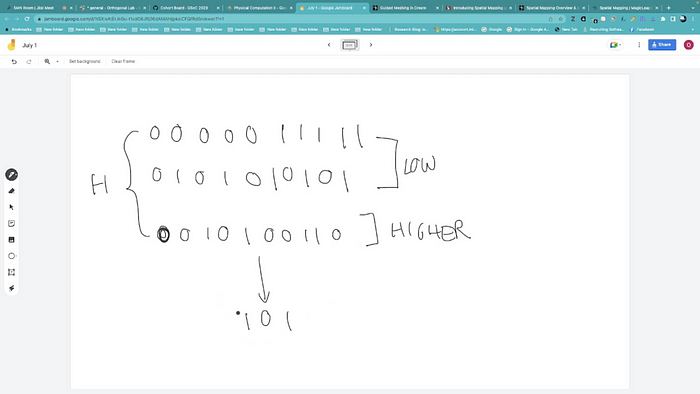
Physical Computation Session II from July 1 (roughly one hour in length)

After taking a break from the topic, our July 15 meeting featured an alternative viewpoint on pancomputationalism. This was made manifest in a shorter discussion on physical computation, with views from Tomasso Toffoli and Stephen Wolfram. We covered Toffoli’s paper “Action, or the funcgability of computation”, which connects physical entropy, information, action, and the amount of computation performed by a system. This paper is of great interest to the group in light of our work and discussions on 4E (embodied, embedded, enactive, and extended) cognition [3]. Toffoli makes some provocative arguments herein, including the notion of computation as “units of action”. A concrete example of this is a 10-speed bicycle, which is not only not a conventional computer, but also has linkages to perception and action. Amanda Nelson found the notion of transformation from one unit into another particularly salient to the distinction between analogue and digital computation. The physical basis of all forms of computation can also be better defined by revisiting “A New Kind of Science” [4], in which Wolfram sketches out the essential components and analogies of a computational system with a physical substrate. We can then compare some of the more abstract aspects of a physical computer with neural systems. This is particularly relevant to engineered systems that include select components of biological networks.

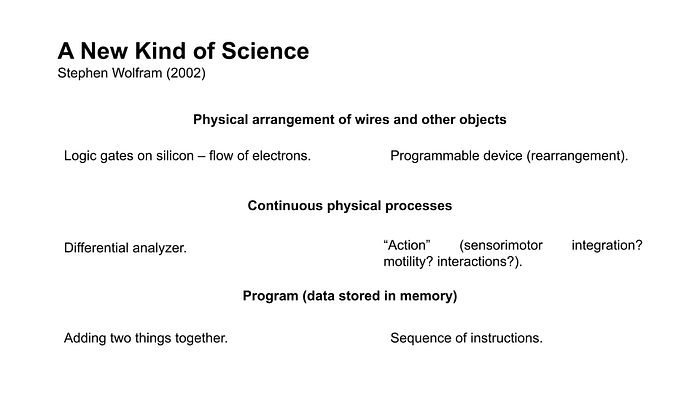
Physical Computation Session III from July 15 (about 15 minutes in length)

The next session followed up on computation in natural systems as well as Wolfram’s notion of universality, particularly in terms of computational models. In particular, Wolfram argues that cellular automata models can characterize universality, which is related to pancomputationalism. Universality suggests that any one computational model can capture system behavior that can be applied across a wide variety of domains. In this sense, context is not important. Rule 30 produces an output that resembles pattern formation in biological phenotypes (the shell of snail species Conus textile), but can also be used as a pseudo-random number generator [5]. In “A Framework for Universality in Physics, Computer Science, and Beyond”, this perspective is extended to understand the connections between computation defined by the Turing machine and a class of model called Spin Models. This provides a framework for universality that is useful form defining computation across the various levels of neural systems, but also gives rise to understanding what is uncomputable. This sessions natural system examples featured computation among bacterial colonies embedded in a colloidal substrate along with computation in granular matter itself. The latter is an example of non-silicon based polycomputation [6].

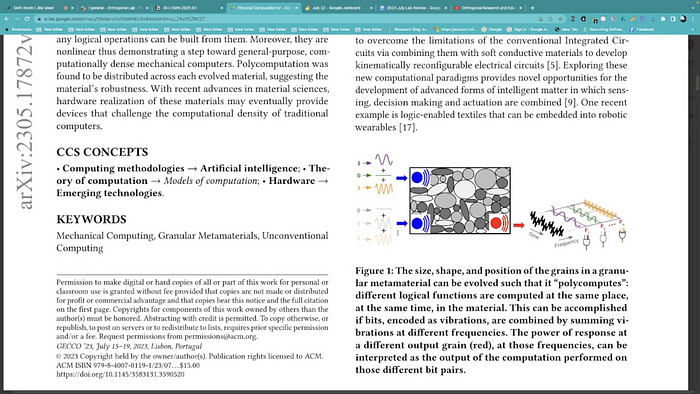
Physical Computation Session IV from July 22 (about 12 minutes in length).

After talking a more extended break from the topic, we returned to this discussion four weeks later (August 19). Our sixth (VI) session occurred in our August 19 meeting, and covered three topics: physical computation and topology, morphological computation, and RNA computing/Molecular Biology as universal computer.

We have discussed category theory before in our discussions on Symbolic Systems and Causality. In this section, we revisited the role of category theory, but this time with reference to Physical Computation. John Carlos Baez and Mike Stay give a tour of category theory’s role in computation via topology. The idea is that category theory forms analogies with computation, which can be expressed on a topological surface/space.

Computable Topology, Wikipedia.

Baez, J. and Stay, M. (2009). Physics, Topology, Logic and Computation: A Rosetta Stone. arXiv, 0903.0340.

Mapping category theory operators to a topological description.

We aslo covered the role of Morphological Computation by reviewing three papers on this form of physical computation that intersects with digital computational representations. Morphological Computation is the role of the body in the notion of “cognition is computation”. One idea that is critiqued with in these papers is offloading from the brain to the body. Offloading is moving computational capacity from the central nervous system to the periphery. If you grab a ball with your hand, you recognize and send commands to grasp the ball, but you must grasp and otherwise manipulate the object to fully compute the object. Thus, this capacity is said to be offloaded to the hand or peripheral nervous system.

Interestingly, offloading and embodiment are integral parts of 4E (Embodied, Embedded, Enactive, and Externalized) Cognition, which itself critiques the brain as computation idea. But as an analytical tool, morphological computation is much more utilitarian than Cognitive Science theory, and is concerned with how the robotic bodies and other mechanical systems interact with an intelligent controller. In non-embodied robotics, body dynamics is treated as noise. But in morphological computation, body dynamics play an integral role in the intelligent system and contribute to a dynamical system.

Muller, V.C. and Hoffmann, M. (2017). What Is Morphological Computation? On How the Body Contributes to Cognition and Control. Artificial Life, 23, 1–24.

Fuchslin, R.M., Dzyakanchuk, A., Flumini, D., Hauser, H., Hunt, K.J., Luchsinger, R.H., Reller, B., Scheidegger, S., and Walker, R. (2013). Morphological Computation and Morphological Control: Steps Toward a Formal Theory and Applications. Artificial Life, 19, 9–34.

Milkowski, M. (2018). Morphological Computation: Nothing but Physical Computation. Entropy, 20, 942.

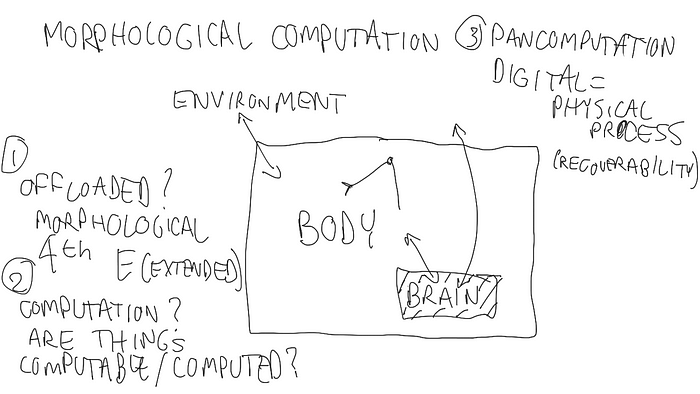
The three insights from our morphological computational discussion.

While these papers do not get too deeply into the role of pancomputation in Morphological Computation, it is implicitly stated and plays a central role in our last topic: RNA computing and Molecular Biology. For more information, see this talk on YouTube and the paper below. Basically, while the pancomputationalism perspective is missing from biology, the structure and potential function of DNA and RNA provide a route to phycial computation.

Akhlaghpour, H. (2022). An RNA-based theory of natural universal computation. Journal of Theoretical Biology, 537, 110984.