Learning on Graphs (LoG) conference recap

 

The Learning on Graphs (LoG) conference took place from December 9-12 and featured a broad diversity of research on Graph Neural Networks (GNNs). GNNs [1] encompass a relatively new area of machine learning research which have a number of interesting connections to applied math and network science. The daily sessions (keynote talks and oral presentations), in addition to the seven workshop sessions, are available from the conference YouTube channel.

GNNs are a way to take data that yield graphical relationships in the real world and analyze then using the power of neural networks. While GNNs are specialized for problems that can be represented as a graph (discrete, interconnected systems), any problem with a set of complex geometric relationships is appropriate for GNNs. While the output of GNNs are typically embeddings (graph topologies embedded in the feature space), some problems require different approaches such as functions or more formal representations.

It is the analysis of these graphical relationships which make it a useful analytical approach. In all their forms, GNNs yield useful representations of graph data partly because they take into consideration the intrinsic symmetries of graphs, such as invariance and equivariance of graph topology with respect to a relabeling of the nodes [2]. Based on what was featured at LoG, GNNs had many potential applications in the biological arena, including precision medicine, drug discovery, and characterizing molecular systems (such as Stefan Gunnemann's (Technical University of Munich) talk in the Friday session).

GNNs can be evaluated using the isomorphism (or k-WL) test, which evaluates whether two graphs are isomorphic. Given that a graph can be drawn from the source data, the source data graph should be isomorphic with the output graph. The Weisfeiler-Lehman heuristic for graph isomorphism can be summarized in the 1-D case as the color refinement algorithm. A related issue in GNN research is algorithmic expressiveness. Expressivity is the breadth of ideas that can be represented and communicated using a particular type of representation. One current challenge of GNNs as they are applied to various problem domains is their ability to be functionally robust. One solution to this is by using GNNs as a generative model. Generating alternate graph representations allows us to use graphons [3], functions that capture different GNN topologies of the same type. The collection of graphs associated with a graphon can then be evaluated. Soledad Villar's (Johns Hopkins) presentation during the Sunday session featured an in-depth discussions of expressiveness and graphons as they relate to GNN performance.

GNNs can be combined with various analytical techniques traditionally used in complex network analysis. One of these involves the analysis of graphical models using tools from network science. These include the use of random graphs and stochastic block models to uncover the presence of topological structure and community formation, respectively. GNNs have ties to category theory as well. The cats.for.ai workshop (October 2022) featured applications of category theory to GNNs. In the Saturday session, Taco Cohen (Qualcomm AI) discussed how the techniques of category theory, monads in particular, can be applied to GNNs. GNNs can also form directed acyclic graphs (DAGs), which are amenable to causal models. 

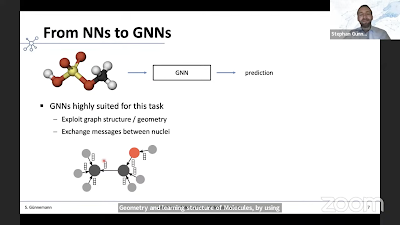
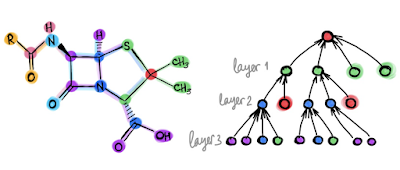
GNNs are constructed using a series of inferential techniques. One technique discussed at LoG is message passing neural networks (MPNNs). Discrete forward passes from node to node (along edges) allow for approximation of the true, original network topology to be reconstructed. MPNN is a standard technique that lends itself to a wide variety of problem domains. The MPNN approach [4] can be extended to directed multigraphs and other types of graphs that capture complex systems, but can suffer shortcomings such as over-smoothing, over-squashing and under-reaching. While message passing has been the standard in the GNN field, continuous methods using approaches inspired by differential geometry and algebraic topology might serve as powerful alternatives [5]. Aside from approximations of real-world networks and graph-like structures, we can also think of GNN outputs in terms of time (capturing delays) and space (capturing translations). GNNs are also well-suited to mapping problems from algorithmic domains, in particular dynamic programming [6].

GNNs are particularly useful for task-specific architectures. The DevoWorm group’s D-GNN work (DevoGraph) is an example of this, being specialized for embryogenetic image processing or capturing biological growth and differentiation processes. But GNNs can also engage in transfer learning, which is the transfer of learned information from one context to another. Successful graph transfer learning is characterized by the reproduction of a graph of a similar but different size, or problems that require changes in network size over time.

From "Do we need deep graph neural networks?" by Michael Bronstein, Towards Data Science, July 20, 2020.

Workshops

Several of the workshops were particularly interesting with respect to some of the points mentioned above. There were also a number of outstanding oral presentations and posters not discussed here, but are worth checking out in the daily session recordings or on OpenReview.

Neural Algorithmic Reasoning (video). GNNs serve as excellent processors (neural networks in latent space) that can be aligned with more traditional algorithms [7]. This recasts many optimization problems as neural representation learning, particularly in cases where optimization algorithms do not represent the system being analyzed in a realistic manner.

Expressive GNNs (video). This tutorial covers a range of techniques that can be used to increase the expressivity of GNNs. Borrowing from areas such as topological data analysis and group theory, there is great potential for a variety of highly effective strategies for improving GNN architectures for a host of problems.

Graph Rewiring (video, web). Graph rewiring is presented as a way to overcome the limitations of the MPNN approach. Rewiring is based on the reconstruction of graph edges from iterative adaptive sampling of the input data. There are a number of different techniques that allow us to evaluate edge relevance using techniques such as diffusion and spectral approaches.

GNNs on TensorFlow (video). This tutorial introduces nascent modelers to implementing their own GNN models in the open-source TF-GNN framework. The tutorial uses heterogeneous input data to show how to implement the GNN and deal with missing label and edge information.

References

[1] Sanchez-Lengeling, B., Reif, E., Pearce, A., and Wiltschko, A.B. (2021). A Gentle Introduction to Graph Neural Networks. Distill, doi:10.23915/distill.00033.

[2] Chen, Z., Villar, S., Chen, L., and Bruna, J. (2019). On the equivalence between graph isomorphism testing and function approximation with GNNs. Proceedings of Neural Information Processing Systems, 32.

[3] Ruiz, L., Chamon, L.F.O., and Ribeiro, A. (2020). Graphon Neural Networks and the Transferability of Graph Neural Networks. arXiv, 2006.03548.

[4] Heydari, S. and Livi, L. (2022). Message Passing Neural Networks for Hypergraphs. arXiv, 2203. 16995.

[5] Bronstein, M. (2022). Beyond Message Passing: a Physics-Inspired Paradigm for Graph Neural Networks. The Gradient, May 7.

[6] Dudzik, A. and Velickovic, P. (2022). Graph Neural Networks are Dynamic Programmers. arXiv, 2203.15544.

[7] Velickovic, P. and Blundell, C. (2021). Neural Algorithmic Reasoning. arXiv, 2105.02761.